Espacio para consultas sobre la Unidad 3: Sistema de Ecuaciones Lineales
Hola, como estas? Te hago unas consultas sobre los ejercicios de la guia 3.
Para el 9b no se me ocurre como empezar a plantear el ejercicio
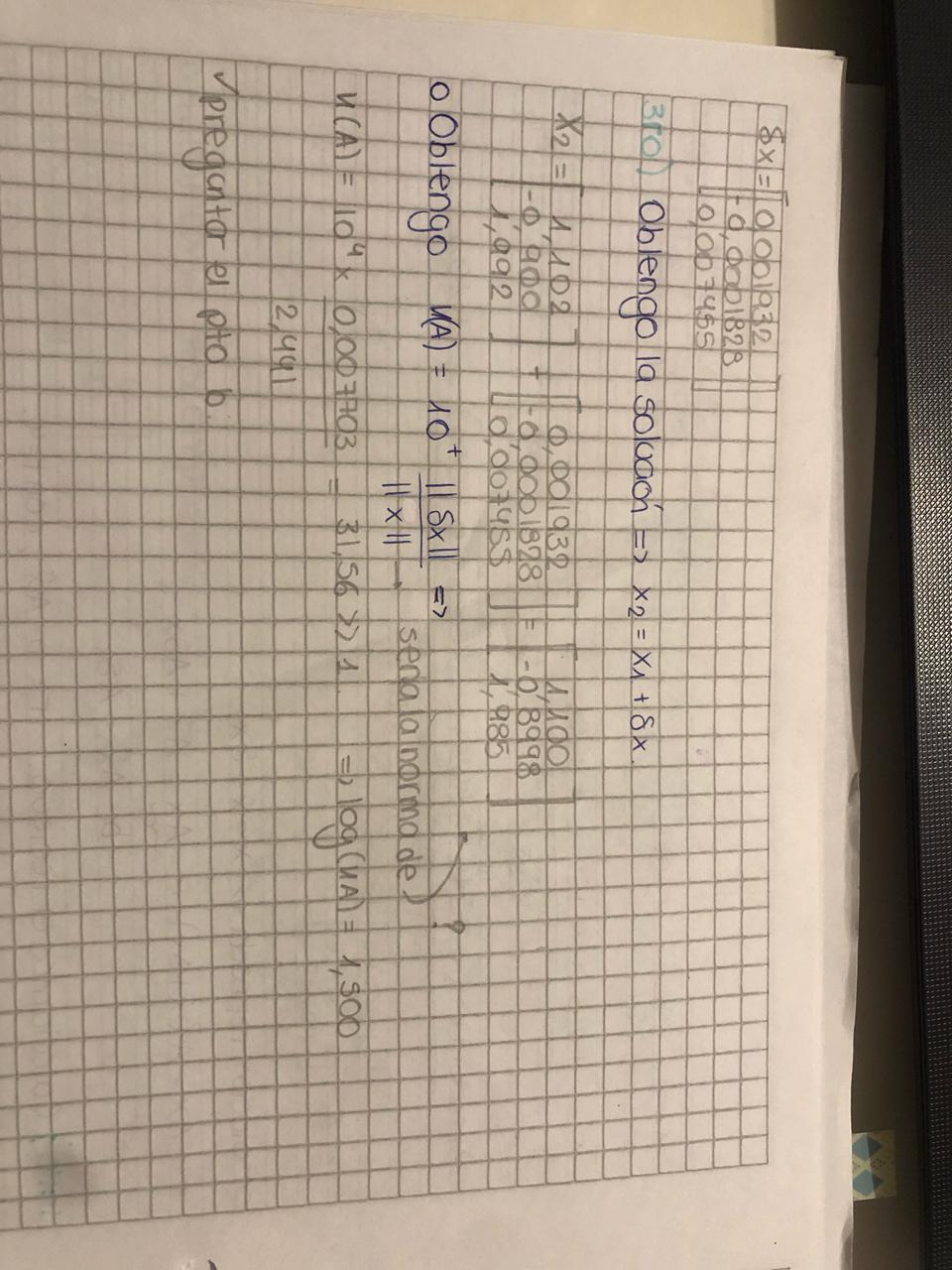
En el c realice un refinamiento iterativo hasta llegar a X2 y para obtener la K(A) seria dividir por la norma de esa nueva solución que encontré con el refinamiento?
En el punto 6, realice un piveotro parcial intercambiando las filas 1 y 2, entonces en el punto b cuando hay que calcular el residuo utilizo mi vector b original o uso el vector b’ (b multiplicado por la matriz de permutación). Y la misma pregunta tengo con la matriz A, utilizo la original o a la que le realice el cambio de filas?
Porque yo utilice el vector b’ y la matriz a la que le realice el intercambio de filas y el residuo me da (0,0)
Para el 9b no se me ocurre como empezar a plantear el ejercicio
En el c realice un refinamiento iterativo hasta llegar a X2 y para obtener la K(A) seria dividir por la norma de esa nueva solución que encontré con el refinamiento?

En el punto 6, realice un piveotro parcial intercambiando las filas 1 y 2, entonces en el punto b cuando hay que calcular el residuo utilizo mi vector b original o uso el vector b’ (b multiplicado por la matriz de permutación). Y la misma pregunta tengo con la matriz A, utilizo la original o a la que le realice el cambio de filas?
Porque yo utilice el vector b’ y la matriz a la que le realice el intercambio de filas y el residuo me da (0,0)

Buenas! respondo sobre el ejercicio 6:
Tené en cuenta que el cálculo de residuo se hace a doble precisión (solamente esa cuenta). Es decir, si se viene trabajando con 3 dígitos, solamente para calcular r = b- A*x1 se deberían que usar 6 dígitos. Acá, en el minuto 6, está explicado: https://youtu.be/10wX4FO43J8. Fijate, si incluso con doble precisión seguís obteniendo r = (0 0), en ese caso no haría falta refinar más.
Es correcto haber usado la matriz permutada A' y el vector independiente permutado b'.
Tené en cuenta que el cálculo de residuo se hace a doble precisión (solamente esa cuenta). Es decir, si se viene trabajando con 3 dígitos, solamente para calcular r = b- A*x1 se deberían que usar 6 dígitos. Acá, en el minuto 6, está explicado: https://youtu.be/10wX4FO43J8. Fijate, si incluso con doble precisión seguís obteniendo r = (0 0), en ese caso no haría falta refinar más.
Es correcto haber usado la matriz permutada A' y el vector independiente permutado b'.
Ejercicio 9:
Punto (a): no hace falta calcular KA, con obtener el valor de x luego de 2 refinamientos está perfecto.
Punto (b), habla de perturbaciones experimentales, esto se refiere a perturbar el sistema modificando levemente los datos de entrada (en este caso el vector independiente, b), para ver cuanto se modifica el dato de salida, en este caso, el vector incógnita x. Entonces, se debe resolver el sistema nuevamente, pero usando (b + delta_b) en lugar de b. Una vez obtenido este nuevo "x_perturbado", se debe usar la formula que se muestra ahi en el ejercicio:
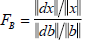
donde dx sería el vector diferencia entre x_original y x_perturbado, y db sería la diferencia entre b_original y b_perturbado. Se calcula la norma de esos vectores diferencia y se divide por la norma de x y de b respectivamente. Los dos factores que aparecen en el numerador y en el denominador de Fb serían como "errores relativos". Basicamente se quiere ver cuanto es afectado x al afectarse b.
Punto (a): no hace falta calcular KA, con obtener el valor de x luego de 2 refinamientos está perfecto.
Punto (b), habla de perturbaciones experimentales, esto se refiere a perturbar el sistema modificando levemente los datos de entrada (en este caso el vector independiente, b), para ver cuanto se modifica el dato de salida, en este caso, el vector incógnita x. Entonces, se debe resolver el sistema nuevamente, pero usando (b + delta_b) en lugar de b. Una vez obtenido este nuevo "x_perturbado", se debe usar la formula que se muestra ahi en el ejercicio:
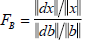
donde dx sería el vector diferencia entre x_original y x_perturbado, y db sería la diferencia entre b_original y b_perturbado. Se calcula la norma de esos vectores diferencia y se divide por la norma de x y de b respectivamente. Los dos factores que aparecen en el numerador y en el denominador de Fb serían como "errores relativos". Basicamente se quiere ver cuanto es afectado x al afectarse b.
Espero que se entienda mas o menos, cualquier cosa consultá nuevamente. Saludos!
Buenas! En clase no vimos SOR, deberíamos hacer esos ejercicios de la guía de todos modos?
Buenas! si, no es complicado. En este video hay un ejercicio resuelto por Jacobi, GS y SOR:
https://youtu.be/YXnkaXj0fJA?list=PLpSEXqDH9rYeS9jHdpqZkxP0MPKZwuH7F (SOR arranca en el min 16.28). Cualquier duda pueden consultar en clase o por aca. Saludos!
https://youtu.be/YXnkaXj0fJA?list=PLpSEXqDH9rYeS9jHdpqZkxP0MPKZwuH7F (SOR arranca en el min 16.28). Cualquier duda pueden consultar en clase o por aca. Saludos!
Hola buenasss, queria consultar acerca del concepto de la p en LU. No me queda claro si p es la matriz identidad con las operaciones que hacemos a la matriz inicial A cuando estamos triangulando hasta que terminamos de triangular o si solamente son las operaciones antes de triangular. Siento que esta concepto no me quedo del todo claro. Muchas gracias y perdon por la molestia!!!
Ya resolvi la duda! Vi un par de ejemplos y creo que me quedo claro. Gracias!
Hola queria consultar acerca del 16, particularmente queria preguntar si al hacer gauss seidel siempre tenemos que resolver en orden el x1 x2 y x3. Porque pense que capaz para mejorar el algoritmo me conviene primero resolver x1 (k+1), despues x3 (k+1) pues solamente usa x1 y no usa x2, dejando para el final x2(k+1). No se si se termina de entender mi duda. Tampoco termino de entender el inciso C, como que leo y no se bien que me esta preguntando, si es que me pueden dar una ayuda con ese, muchas gracias saludos
Hola,
1) Consulta sobre la mejora del algoritmo. Podes cambiar el orden pero para no marearte, cambiaría el nombre de las variables antes de empezar a iterar.
Igualmente, el ejercicio no apuntaba a eso sino a la forma de despejar x1, x2 y x3 de cada ecuación, ya que no hace falta despejar x1 de la primera ecuacion, x2 de la segunda, etc. Se puede elegir qué variable se despeja de qué ecuacion.
2) Consulta sobre el inciso c). Te pide que evalúes cuántos digitos de precisión tiene la solución obtenida, y si se verifica que
- el error de tu solución: podes calcular el error exacto como tu resultado obtenido en (a) menos la solución exacta, o sacarlo a partir de los dígitos significativos que obtuviste.
cumple ser menor a - la estimación del error: calculada como la diferencia entre 2 soluciones sucesivas (sería las ultimas 2 en las iteraciones del inciso anterior)
Ahhh claro entiendo, ahora releyendo y con tu comentario me quedo mas claro que pedia, voy a revisarlo. Muchas gracias
Hola tambien tenia consultas acerca del D del ejercicio 16 jaja, perdon que no lo puse en el otro comentario. Es que ni el c ni el d me terminaron de cerrar, como es que puedo ver como afecta la pertubacion sin necesidad de hacer gauss seidel todo de nuevo?
Había que hacer Gauss Seidel todo de nuevo y fijarse cuanta diferencia había en la solución obtenida con el dato de entrada original con la solución obtenida con el dato de entrada perturbado.
