Espacio para consultas sobre la Unidad 8: Ecuaciones Diferenciales
Buenas profe! tenía una duda con el ejercicio 20 de la guía. Te adjunto foto de como discretice el problema, a la hora de avanzar con el proceso no me muevo de los valores semilla 0 y 1. Quería saber donde estaba el error, gracias!

dw/dt = - u (1) --> fw (t, u, w) = -u
du/dt = w (2) --> fu (t, u, w) = w
Entonces la discretización quedaría:
un+1 = un + k * wn
wn+1 = wn + k * (-un)
y tenes que arrancar con u0 = 0 y w0 = 1
Saludos!
Hola Marina, como estas? Te hago unas preguntas sobre los ejercicios 5 y 6 de la guia.
En el ejercicio 5 para usar Euler inverso tengo q hacer F(Un+1) pero nose como hacer para averiguar ese Un+1 cuando n=0. Y otra cosa, como paso de calculo estaría bien usar k=0,1 si no me especifican ningún otro?
Y en caso de seguir con el ejercicio hasta donde debería aproximar mi U, es decir cuando dejo de hacer las cuentas si no me aclara.
Y en el ejercicio 6, te pide resolverlo por RK2, y también me quede trabada en n=0, porque cuando hago el paso del corrector es decir el de Un+1, no se donde donde averiguo tn+1/2. Supongo q lo tendría que sacar por el paso de calculo pero tampoco me lo dan, entonces no se cual usar o en q me tengo q basar para elegirlo.
Muchas gracias
Ejercicio 5: en la materia en los ultimos cuatris no se están dando métodos implicitos como Euler inverso. En los métodos implícitos la resolucion no es directa por esto de que se tiene un+1 a ambos lados, entonces hay que resolver una ecuación. Salteenlos o resuélvanlos con cualquiera de los explícitos.
Ejercicio 6: t_n+1/2 sería el t que queda justo en el medio entre tn y tn+1. Por ejemplo, en este ejercicio, si tomamos h=0.1, en n=0: tn=0, tn+1 = 0.1, tn+1/2=0.05.
Holaa, como estas?? Te hago una pregunta sobre algunos ejercicios de la guia.
En el 8 te pide estimar el tamaño de la malla para obtener una precisión 10^-4, como puedo conseguir eso?

En el 14, nose como demostrar como se refleja el orden de precisión del esquema en la reducción del error de truncamiento.

En el 17 nose como darme cuenta cual seria un metodo numérico apropiado para resolver ese sistema de ecuaciones diferenciales.
Ejercicio 8.
Para obtener una precisión de 10^-4, podríamos pedirle al resultado que tenga un error menor a 0.5*10^-5. Se sabe que Euler es de orden 1, por lo tanto si el paso disminuye en una razon k, el error tambien disminuye en la misma razón aprox (el clasico ejemplo, si se disminuye h en 1/2, disminuye 1/2 el error). Entonces se podría resolver para un paso cualquiera h0, estimar el error E0 y luego buscar un paso h1 que cumpla con tener error menor al requerido, planteando lo siguiente:
error con h0: E0.
Por ser de orden 1:
error con h1 = h0/k: E1 = E0/k
E1 < 0.5*10^(-5) --> E0/k < 0.5*10^(-5) --> entonces teniendo E0 se puede despejar k, y con eso sacar h1 como h0/k
1) calcular u(0.1) con Euler y un h muy chico.
3) usar Euler para 2 pasos distintos y hacer extrapolación de RIchardson
Lo del orden de precisión sería el mismo concepto que en el 8, solo que en este caso te dan directamente la solución exacta, entonces es más facil de calcular. Entonces:
1) sacas las soluciones con k = 0.1 y k = 0.05
2) sacas el error para ambas comparando contra la exacta
3) te fijas que en cada caso, como 0.05 = 0.1 / 2, el error con 0.05 debería ser aproximadamente (error con 0.1) /2.
Buen dia marina. Queria saber si estaba bien resuelto porque cuando armo la matriz no utilizo x4. Porque si tengo que usarlo no se en que ecuacion ponerlo.
Saludos
- Tenes 5 nodos --> 5 incognitas.
- Las condiciones de borde te dan información sobre y0 y y4 --> 2 datos.
- 5 incognitas - 2 datos = 3 ecuaciones --> te queda un sistema de 3x3.
En wolfram podes chequear la solucion del sistema: https://www.wolframalpha.com/input?i=%7B%7B-2%2C1%2C0%7D%2C%7B1%2C-2%2C1%7D%2C%7B0%2C1%2C-4%2F3%7D%7D*%7B%7By1%7D%2C%7By2%7D%2C%7By3%7D%7D+%3D+%7B%7B0*0.5%5E2%7D%2C%7B1*0.5%5E2%7D%2C%7B0*0.5%5E2-1%2F3%7D%7D
(para y1 e y2 da un numero muy chico en lugar de 0 por error de redondeo, si lo haces a mano da 0, pero para darse una idea está bueno)
Saludos!
 Hola, como estas? Quería saber si había hecho bien el ejercicio, mas que nada para saber si interprete la idea de pasar a primer orden la ecuacion. Muchas gracias
Hola, como estas? Quería saber si había hecho bien el ejercicio, mas que nada para saber si interprete la idea de pasar a primer orden la ecuacion. Muchas gracias
Llamas z a du/dt, eso está perfecto. El sistema te queda:
du/dt= z
dz/dt = -2u
Antes de seguir, aclaro que no recomendaría usar la misma letra de la variable original en la discretización para no marearse. Para no confundirte, voy a usar Z para z y U para u:
la función igualada a la du/dt es la función usada para discretizar u, por lo tanto:
Un+1 = Un + h*Zn
y la función igualada a la dz/dt es la función usada para discretizar z, por lo tanto:
Zn+1 = Zn + h*(-2Un)
La discretización correcta serían esas 2 ecuaciones juntas.
Hola profe, te molesto con otra pregunta. En el ejercicio 6 te pedia analizar la estabilidad usando RK2. Llegue a estas expresiones pero me trabe. Deberia de reemplazar en la 2da ecuación al delta* por lo que me dio anteriormente y ahí encontrar el deltan+1/deltan ? O como seria el procedimiento cuando me quedan dos ecuaciones para analizar la estabilidad? Muchas gracias!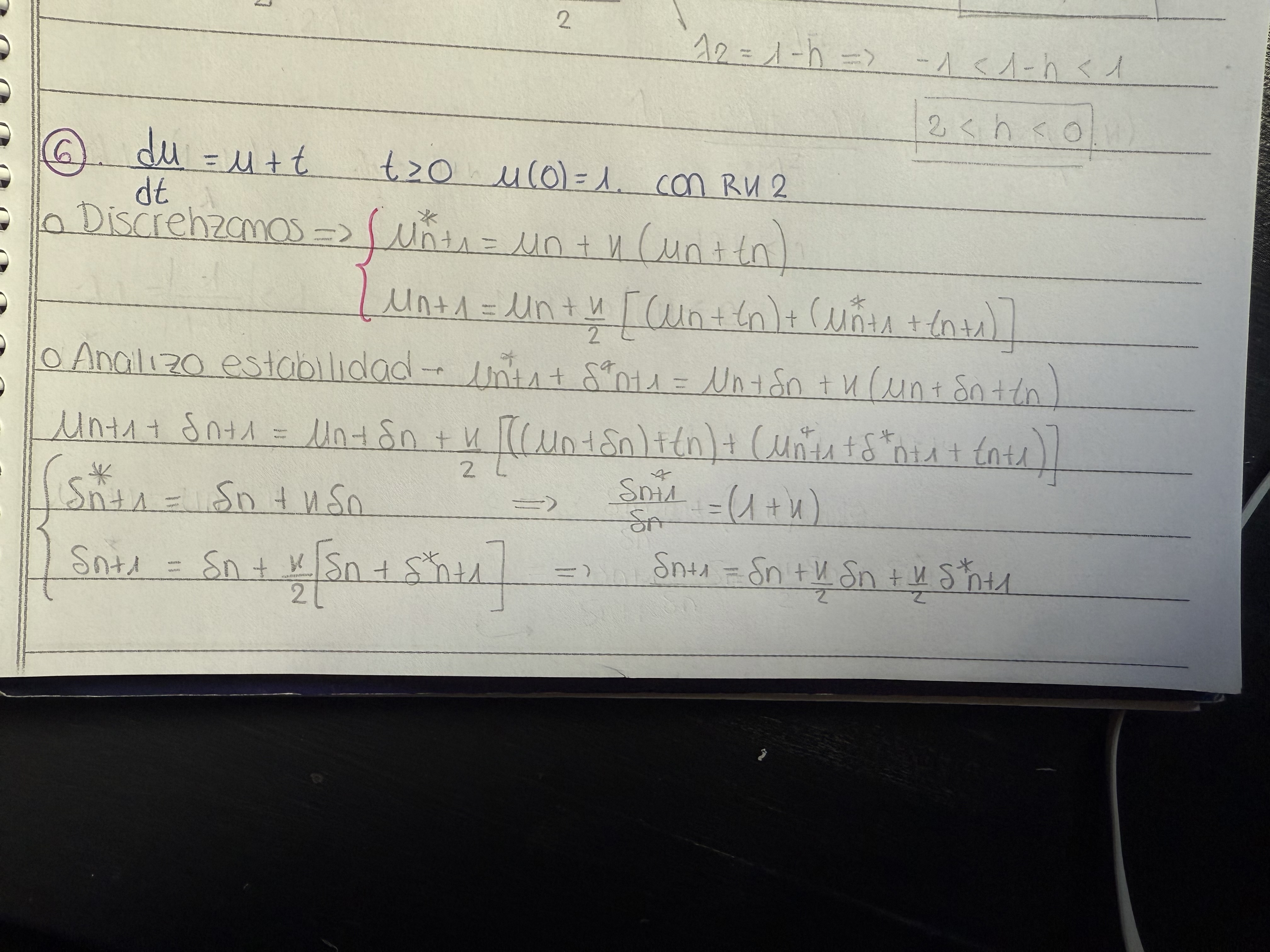
El resultado a chequear, pero el procedimiento iría por acá:
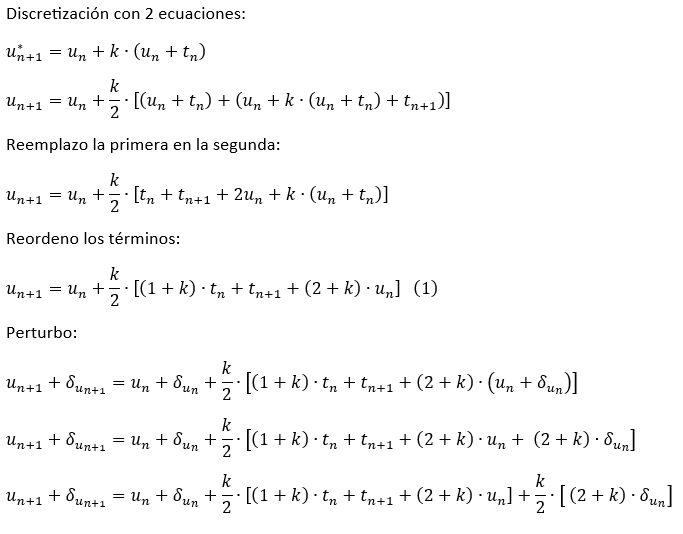

Hola profe, te queria consultar acerca de este ejercicio, te pregunto si esta bien hecha la discretizacion y se que tengo q hacer una perturbacion para sacar la estabilidad y a partir de eso sacar el paso h, el problema q tengo es q me da q h debe ser menor que cero y no entiendo si a eso apunta el ejercicio o si estoy haciendo algo mal



Entiendo que adentro del parentesis dice 2y+t, no 2y+1, pero si fuera un 1 el procedimiento es análogo.
El reemplazo es correcto. dy/dt =z, entonces queda:
dy/dt = z
dz/dt = 2 * (2y+t) = 4y+2t
Pero la discretización está mal. La primera función, que vos llamaste f1, está igualada a la derivada de y, por lo que es la función con la que se aproximará la pendiente de la función y, y por lo tanto que se usa para discretizar a y. Análogamente, la segunda función, 4y +2t, se usa para discretizar a z. Entonces, usando
"Y" para discretizar "y", "Z" para discretizar "z" con Euler quedaría:
Yn+1 = Yn + h*Zn
Zn+1 = Zn + h*(4Yn+2tn)
Hola profe! Perdón que moleste. Mi pregunta es la siguiente: en aquellos ejercicios donde la discretización es un sistema de ecuaciones (por ejemplo el 3, donde te dan la derivada segunda) ¿cuál es la manera de chequear la estabilidad? ¿Se deben perturbar ambas ecuaciones y que ambos g sean menores a 1? ¿O se debe buscar los autovalores de la matriz del sistema?
Muchas gracias!
la idea nunca es reemplazar de forma automática sino que se entienda qué estamos haciendo.
Cuando se discretiza una ecuacion diferencial en un intervalo [x0,xf], se toma un dominio continuo, que va desde x0 hasta xf, y se lo divide en pasos iguales y discretos, que valen h. Los puntos discretizados del dominio son: x0, x0+h, x0+2h, x0+3h.... así hasta llegar a xf.
Entonces la fórmula general, sería xi = x0 + h*i . x=h*i solo si x0=0. Si no, hay que sumarle el x0.
Por ejemplo, si estamos considerando un intervalo que va de 2 a 4, y queremos tomar pasos de h=0.5, los x para los que se quiere calcular cuánto vale la función son: 2, 2.5, 3, 3.5, 4. Entonces si queremos pensar en la fórmula, los xi que vamos a considerar pueden escribirse como
xi = x0 + h*i, es decir,
Para i=0, x0=2.
Para i=1, x1=x0+h*1= 2+ 0.5 = 2.5.
Para i=2, x2=x0+h*2= 2+ 0.5*2=3
y así sucesivamente hasta llegar a 4.
No tendría sentido usar x*i = 0, 0.5, 1, 1.5, ...etc, si el dominio es [2,4]
Saludos.

Hola profe, me surgio una duda con este ejercicio, no sabria como usar el dato de dy/dx(x=3) =-y(x=3) porque intente reemplazar la derivada por yi+1-yi-1/(2h) pero me quedaria una incognita. Segun encontre en internet se utiliza otra formula para la derivada porque estoy en un extremo y no en un punto interno. Esta es la formula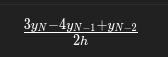
Seria correcto usar esta formula? o como se usa el dato?
Buenas! Para PVC en los casos como el ejercicio 30 que piden un "método directo" se refieren a utilizarlos métodos que usan lo visto en la unidad 7 de diferenciación? O se refieren a que, una vez planteada la matriz del sistema esta misma debe ser resuelta mediante un método directo? Gracias
