Hola profe, con Tomás tenemos una duda. Nos olvidamos de mandarte antes pero seguimos con la misma duda. En clasificación buscamos estimar la P(Y|X) de tal manera que:
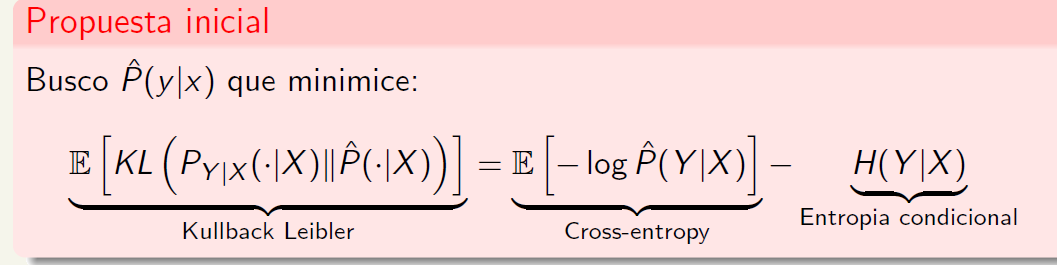
Nuestra duda es que si desarriollamos la KL ya obtenemos la crossentropy - la entropia condicional. Entonces no entendemos por que se toma la esperanza de la KL y encima a eso se le vuelve a llamar KL. Entendemos que la KL dentro de la esperanza depende de X ya que son densidades |X y que esa esperanza la tomamos sobre X. pero si desarrollamos sin la esperanza nos queda de todos modos los términos de la derecha, entonces si agregamos la esperanza, nos queda la espreanza de la cross entropy .- entropia.
Gracias y saludos.

