Guia 2

Dudas ejs 1 y 9

Dudas ejs 1 y 9

de RIOS CASANDRA -
Número de respuestas: 3

Buenas tardes profe, estamos terminando la guía con un compañero y comparando resultados nos surgieron un par de dudas en común que ninguno pudo despejarle al otro. 

Ejercicio 1)

El último ítem pide calcular el error bayesiano expresando el resultado de las integrales en función de phi(•). Viendo las diapositivas en Error Bayesiano es 

1 - E[max_y PY|X(y|X)]

A nosotros nos quedaron así ambas funciones de probabilida condicional:



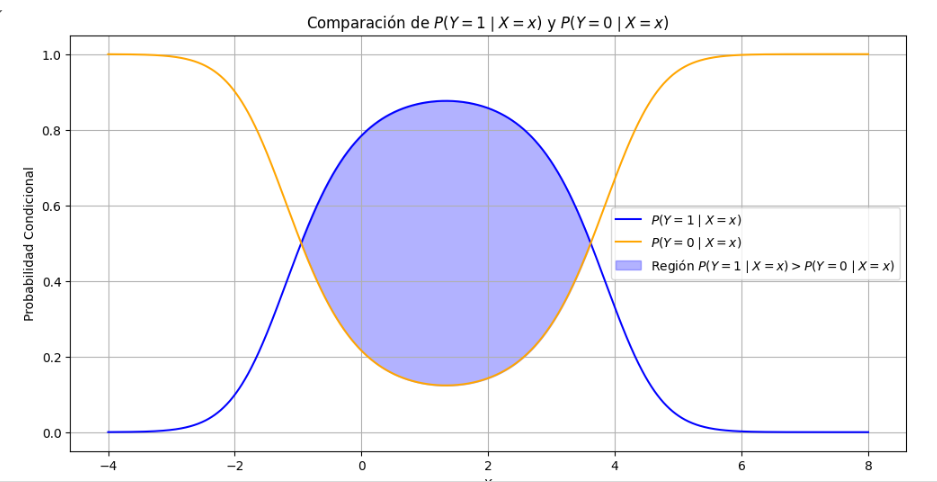
Entonces lo que entendimos que debemos hacer para la parte de la esperanza en el Error Bayesiano es calcular la esperanza teniendo en cuenta que en cada intervalo de X una de las dos distribuciones es máxima. Pero pide expresar el resultado de las integrales en función de normales estándar. No entendemos bien cómo hacer esto ya que quedaría una integral de multiplicaciones y divisiones de gaussianas entonces no sabemos bien por qué lado encarar este ejercicio. 

Ejericico 9) 
En este ejercicio nos pasó que las soluciones del problema dual y primal nos dan distintas, tanto relajando márgenes como no.  ¿Deberían dar igual? Dejamos foto de los ítems a y b en orden a continuación.  Además, relajando o no márgenes, nos pasa con los problemas duales que los márgenes quedan muy pegados a la frontera de decisión. ¿Alguna idea que explique estos resultados?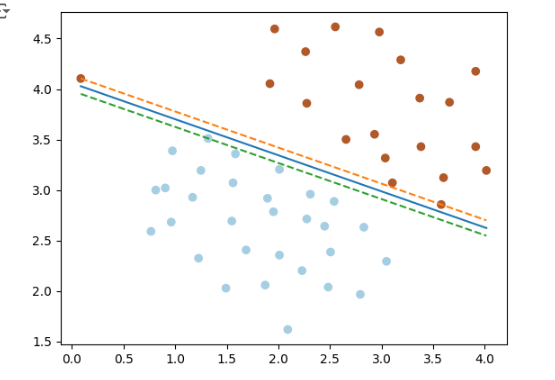



Gracias y saludos, Casandra y Tomás. 

En respuesta a RIOS CASANDRA

Re: Dudas ejs 1 y 9

de VERA MATIAS ALEJANDRO -
Hola gente,

1) Como vos bien decís, te va a quedar la integral (que viene de la esperanza) dividida en 3 pedazos: de -infinito al primer punto donde se cruzan las curvas (ahí calculo la esperanza de la curva naranja), entre los dos cruces (ahí la azul) y de ese último cruce a +infinito. Cada una de esas 3 integrales ¿que tiene adentro? Haciendo bayes lo simplifico
$$\int_a^bf_X(x)P_{Y|X=x}(c)dx=\int_a^bP_Y(c)f_{X|Y=c}(x)dx=P_Y(c)\mathbf{P}(a<X<b|Y=c)$$

donde "a", "b" y "c" serán distintos en cada integral. De esta manera te queda la probabilidad sobre una normal y estandarizando podés obtener lo pedido. Otra manera de hacerlo es simplificar la expresión del error bayesiano en genérico y reemplazar al final. Si te interesa esto último podés usar como referencia este video (
) a partir del minuto 28 más o menos.

9) Puede ser que por una cuestión numérica den un poquito distintos, pero no debería ser apreciable a ojo. En tus imágenes se ve que algo no está andando. Pueden pegarme el pedazo de código para que lo mire más en detalle, pero me animo a proponer una posible fuente de error.
* Lo primero a chequear es como armaste el w y el b: A diferencia de los problemas primales que ya te los devuelven como solución, los duales te devuelven los alphas y hay que laburar con ellos para armar el w y el b.
* En particular, para armar el b ustedes tienen que determinar cuáles son los vectores soportes. Uno diría: eso es fácil, fijarte si alpha es o no =0. El tema es que por cuestiones numéricas los ceros no son tan ceros. Yo propondría decir que los vectores soportes son los que tiene alpha>epsilon, con un epsilon chiquito (por ejemplo 1e-7).
Si el error no era ninguna de estas dos opciones, pasenme algo de código y voy viendo más en detalle.

Cualquier cosa vuelvan  a preguntar.
Saludos
En respuesta a VERA MATIAS ALEJANDRO

Re: Dudas ejs 1 y 9

de RIOS CASANDRA -
Buen día profe.
Entendimos lo del ejercicio 1, genial gracias.
Con respecto al 9, sí estábamos teniendo todo eso en cuenta. Finalmente descubrimos lo que nos estaba pasando en los problemas duales.
Los w1 y w2 los estábamos calculando como:
w1 = np.sum(alpha*y*X1)
w2 = np.sum(alpha*y*X2)

Pusimos los 3 vectores con el mismo formato agregando a X1,2 y alpha un [:,newaxis]. Así la suma entendemos que dio bien porque de esta manera visualmente las soluciones duales y primales dan "iguales".
Gracias y saludos.