
{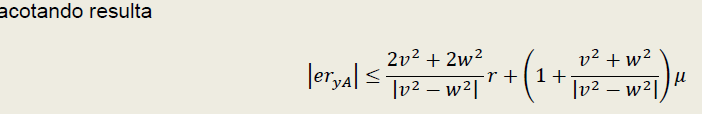
buenos días, en este ejercicio no entiendo porque el termino de estabilidad queda V^2 +W^2. Haciendo las cuentas me da que tiene que quedar V^2-W^2. Si lo que digo es correcto, el Te quedaría en 2?
Saludos

{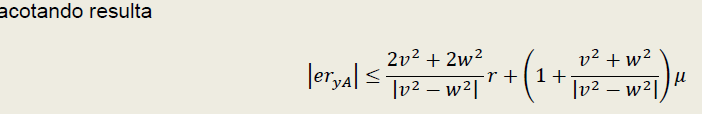
buenos días, en este ejercicio no entiendo porque el termino de estabilidad queda V^2 +W^2. Haciendo las cuentas me da que tiene que quedar V^2-W^2. Si lo que digo es correcto, el Te quedaría en 2?
Saludos