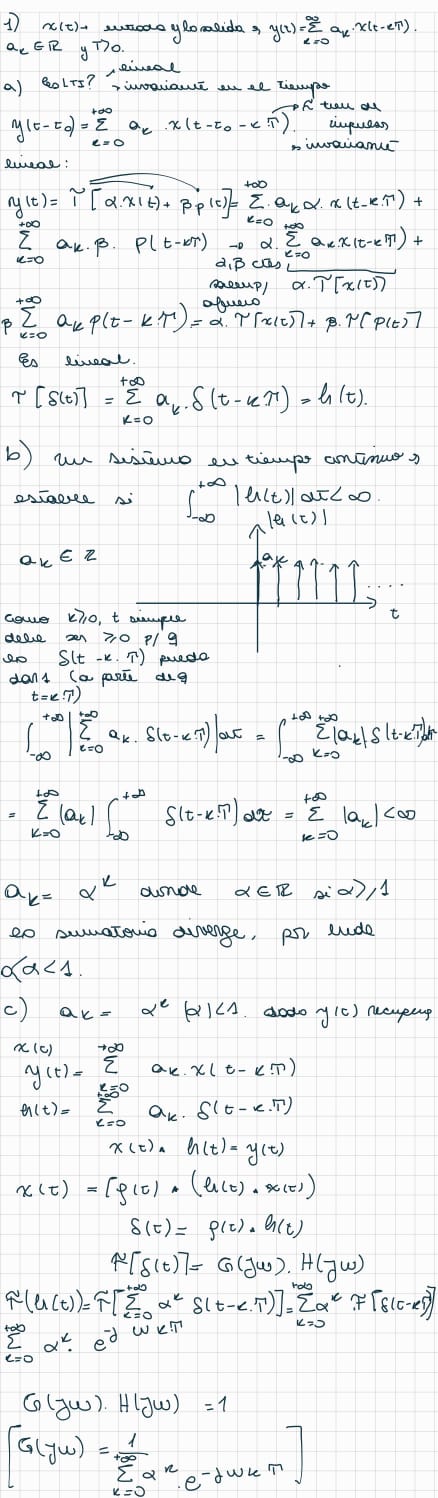
Hola Julieta!, como estas?. El ejercicio esta bien planteado. Ojo cuando trabajas con módulos, el modulo de la suma NO es la suma de los módulos (es menor a la suma de los módulos).
Finalmente el item c)
Para que un sistema pueda ser implementando mediante ecuaciones diferenciales, su H(w) tiene que ser un cociente de polinomios en w. Te pongo un ejemplo pero generalizar el concepto es muy simple:
y'(t) + y(t) = 2x'(t) + x(t) transforma a jwY(w) + Y(w) = 2jwX(w) + X(w) => Y(w)/X(w) = H(w) = (1 + 2jw) / (1 + jw)
Como ves, se obtuvo un cociente de polinomios en w.
En tu caso G(w) no tiene esa forma, con lo cual el sistema no puede ser implementado de esta manera.
En tiempo discreto hay una idea similar respecto a las ecuaciones en diferencias, solo que no quedan cocientes de polinomios en la frecuencia, sino que cocientes de sumas de exponenciales (esto sucede ya que el
desplazamiento en n implica el producto por una exponencial). Cualquier otra pregunta, no dudes en consultar, saludos.